I. Inngangur
Vatn getur kveikt á kertum, er það satt? Það er satt!
Er það satt að snákar séu hræddir við realgar? Það er rangt!
Það sem við ætlum að ræða í dag er:
Truflanir geta bætt mælingarnákvæmni, er það satt?
Við venjulegar aðstæður eru truflanir náttúrulegur óvinur mælinga. Truflanir draga úr nákvæmni mælinga. Í alvarlegum tilfellum verða mælingar ekki framkvæmdar eðlilega. Frá þessu sjónarhorni geta truflanir bætt nákvæmni mælinga, sem er rangt!
En er þetta alltaf raunin? Eru til aðstæður þar sem truflanir draga ekki úr mælingarnákvæmni heldur bæta hana?
Svarið er já!
2. Samningur um íhlutun
Í samanburði við raunverulegar aðstæður gerum við eftirfarandi samkomulag um truflunina:
- Truflanirnar innihalda ekki jafnstraumsþætti. Í raunverulegri mælingu eru truflanirnar aðallega riðstraums truflanir og þessi ályktun er rökrétt.
- Í samanburði við mælda jafnspennu er truflunarvíddin tiltölulega lítil. Þetta er í samræmi við raunverulegar aðstæður.
- Truflun er reglubundið merki, eða meðalgildið er núll innan ákveðins tíma. Þetta gildir ekki endilega í raunverulegri mælingu. Hins vegar, þar sem truflunin er almennt riðstraumsmerki með hærri tíðni, þá er fyrir flestar truflanir eðlilegt að meðalgildið sé núll yfir lengri tíma.
3. Mælingarnákvæmni við truflanir
Flest rafmagnsmælitæki og mælar nota nú AD-breyta og mælingarnákvæmni þeirra er nátengd upplausn AD-breytisins. Almennt séð hafa AD-breytar með hærri upplausn meiri mælingarnákvæmni.
Hins vegar er upplausn AD alltaf takmörkuð. Miðað við að upplausn AD sé 3 bitar og hæsta mælingarspennan sé 8V, þá jafngildir AD breytirinn kvarða sem er skipt í 8 deilur, hver deiling er 1V. er 1V. Mælingarniðurstaða þessa AD er alltaf heiltala, og tugabrotshlutinn er alltaf borinn eða hafnaður, sem er gert ráð fyrir að sé borinn í þessari grein. Að bera eða hafna mun valda mælivillum. Til dæmis er 6,3V stærra en 6V og minna en 7V. Mælingarniðurstaða AD er 7V, og það er 0,7V villa. Við köllum þessa villu AD skammtafræðilegrar villu.
Til þæginda fyrir greininguna gerum við ráð fyrir að kvarðinn (AD breytir) hafi engin önnur mælivillur fyrir utan AD magngreiningarvilluna.
Nú notum við tvo eins kvarða til að mæla jafnspennurnar tvær sem sýndar eru á mynd 1, bæði án truflana (kjörstaða) og með truflunum.
Eins og sést á mynd 1 er raunveruleg mæld jafnstraumsspenna 6,3V og jafnstraumsspennan á myndinni vinstra megin hefur engar truflanir og er fast gildi. Myndin hægra megin sýnir jafnstrauminn sem riðstraumurinn truflar og það er ákveðin sveifla í gildinu. Jafnstraumsspennan á myndinni hægra megin er jöfn jafnstraumsspennunni á myndinni vinstra megin eftir að truflunarmerkið hefur verið fjarlægt. Rauði ferningurinn á myndinni táknar umbreytingarniðurstöðu AD-breytisins.

Tilvalin jafnspenna án truflana
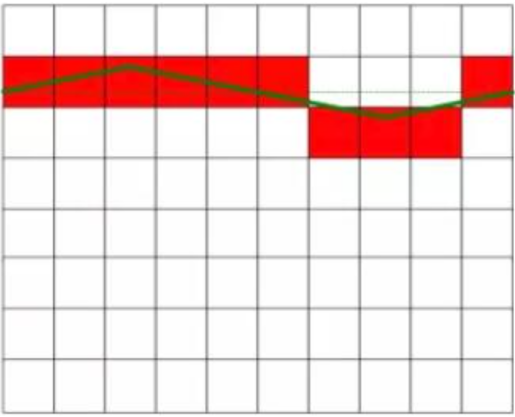
Setjið truflandi jafnspennu með meðalgildi núlls
Gerðu 10 mælingar á jafnstraumnum í tveimur tilfellum á myndinni hér að ofan og reiknaðu síðan meðaltal mælinganna 10.
Fyrsta kvarðinn vinstra megin er mældur 10 sinnum og mælingarnar eru þær sömu í hvert skipti. Vegna áhrifa AD-kvantunarvillunnar er hver mæling 7V. Eftir að meðaltal 10 mælinga hefur verið reiknað er niðurstaðan enn 7V. AD-kvantunarvillan er 0,7V og mælingarvillan er 0,7V.
Annar kvarðinn hægra megin hefur breyst verulega:
Vegna mismunar á jákvæðu og neikvæðu spennunni í trufluninni og sveifluvíddinni er AD-kvantunarvillan mismunandi á mismunandi mælipunktum. Við breytingu á AD-kvantunarvillunni breytist niðurstaða AD-mælingarinnar á milli 6V og 7V. Sjö af mælingunum voru 7V, aðeins þrjár voru 6V og meðaltal 10 mælinganna var 6,3V! Villan er 0V!
Reyndar er engin villa ómöguleg, því í hlutlægum heimi eru engar strangar 6,3V! Hins vegar eru til:
Ef engin truflun er til staðar, þar sem hver mælinganiðurstaða er sú sama, þá helst villan óbreytt eftir að meðaltal mælinga hefur verið reiknað út 10 sinnum!
Þegar viðeigandi truflun er til staðar, eftir að meðaltal 10 mælinga hefur verið reiknað, minnkar AD-kvantunarvillan um nokkrar stærðargráður! Upplausnin batnar um margar stærðargráður! Mælinákvæmnin batnar einnig um margar stærðargráður!
Lykilspurningarnar eru:
Er það það sama þegar mæld spenna er önnur gildi?
Lesendur gætu viljað fylgja samkomulagi um truflanir í öðrum hlutanum, tjá truflanirnar með röð tölulegra gilda, leggja truflanirnar ofan á mælda spennu og reikna síðan mælingarniðurstöður hvers punkts samkvæmt burðarreglu AD-breytisins og reikna síðan meðalgildið til staðfestingar, svo framarlega sem truflunarvíddin getur valdið því að mælingin eftir AD-kvantificering breytist og sýnatökutíðnin er nógu há (breytingar á truflunarvídd hafa umskiptaferli, frekar en tvö gildi jákvæð og neikvæð), og nákvæmnin verður að bæta!
Hægt er að sanna að svo lengi sem mæld spenna er ekki nákvæmlega heiltala (hún er ekki til í hlutlægum heimi), þá verður til AD-kvantunarvilla, óháð því hversu stór AD-kvantunarvillan er. Svo lengi sem sveifluvídd truflunarinnar er meiri en AD-kvantunarvillan eða meiri en lágmarksupplausn AD, þá mun það valda því að mælinganiðurstaðan breytist á milli tveggja aðliggjandi gilda. Þar sem truflunin er jákvæð og neikvæð samhverf, eru stærð og líkur á lækkun og hækkun jafnar. Þess vegna, þegar raunverulegt gildi er nær hvaða gildi, eru líkurnar á því að hvaða gildi birtist meiri, og það verður nálægt hvaða gildi eftir meðaltal.
Það er að segja: meðalgildi margra mælinga (meðalgildi truflunar er núll) verður að vera nær mælingunni án truflana, það er að segja, með því að nota AC truflunarmerki með meðalgildi núll og meðaltal margra mælinga er hægt að draga úr samsvarandi AD kvantifiseringsvillum, bæta upplausn AD mælinga og bæta mælingarnákvæmni!
Birtingartími: 13. júlí 2023




